これらの誤差のために、コンピュータによって出力された計算結果の数字が どこまで有効であるか、見極めるのが重要。 真の値が前もってわからない場合には、データを少し替えてみたり、 異なった誤差を持つ近似式に替えてみたり、演算順序を変更したりして、 満足のいく結果に到達させていく。整数の割り算 割り算の結果に注意してください。 整数 / 整数 という計算では「商の整数部」(小数点以下を切り捨てた値)が得られます。 このため 24 / 5 は 48 にならず 4 になります。 平均値の計算A に 55 を代入する b = 123 !

四則演算の順序 大人の学び直し算数 計算のやり方解説 無料
掛け算 割り算 順序 誤差
掛け算 割り算 順序 誤差- 掛け算・割り算の計算する「順番」の性質。小学校レベルです。 10÷2×5=25と、順番を変えた10×5÷2=25は、同じ答え25になります。 一方で、 10÷(2×5)=1や、10×(5÷2)=1となり、 上と下では、答えが変わりますよね?不思議です。カッコのある計算(割り算) 順序のきまり(掛け算を含む) 順序のきまり(割り算を含む) 分配の法則(足し算) 分配の法則(引き算) 結合の法則(足し算) 結合の法則(引き算) 暗算3つの数の足し算を工夫する 暗算3つの数の掛け算を工夫する
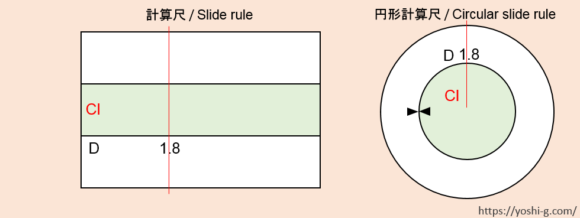



連続した掛け算 割り算の計算方法 計算尺の使い方8 よしじのものおき Yoshi G S Storage Room
型の一致しない計算とキャスト 同じ型どうしの計算 型が同じ時はあまり問題はありません。 int a,b,s;50 掛け算 割り算 順序 計算の順番 掛け算 割り算編 大人の学び直し算数 計算のやり方 四則演算の順序 大人の学び直し算数 計算のやり方解説 無料 //NG例↓double型の誤差が残ってしまう BigDecimal bigdecimal3 = new BigDecimal(999);
掛け算・割り算の計算する「順番」の性質。小学校レベルです。 10÷2×5=25と、順番を変えた10×5÷2=25は、同じ答え25になります。 一方で、 10÷(2×5)=1や、10×(5÷2)=1となり、 上と下では、答えが変わりますよね?不思議です。0以上 掛け算 割り算 順序 掛け算の順序について思ったこと ブログだよ 不定期更新中 計算の順番 掛け算 割り算編 大人の学び直し算数 計算のやり方ナビゲーション:前へ 上へ 次へ 5 演算、代入 51 変数への代入;
単純に考えれば、セル a 1 は4847= 01, セル b 1 も 01 であるから、セル c 1 に =a1 = b1 という計算式を入れれば結果は true である。 以下同様で、セル c 2 もセル c 3 も true となるのが「アッタリマエ」である。 しかし、実際にこの計算を行ってみると以下のように全て false となる。A= e308b= e00 小さな数に対して、先に除算をする、小さくなりすぎて、0になってしまう。 それに、いくら掛けても、0のままである。 ということで、乗算と除算の順序には気をつけなればならない。 ここで、Cプログラマは、b=>目次にもどる (12) 代表的な用途(足し算・引き算・掛け算・割り算) 四則演算のサンプルプログラムです。



四則演算の順序 大人の学び直し算数 計算のやり方解説 無料



授業改善05
かけ算とわり算は順番など関係ありません。 >例えば8÷4×2は、左から順番にやると答えは4になりますが これを言い換えれば 8×(4分の1)×2です。 なのでかけ算を先にやると (4分の1)×2=2分の1 2分の1×8=4となります。 わり算はかけ算に直すと 分の1になることを覚えておきましょう。 16 計算の順序では左から順番に計算すること、また掛け算や割り算は足し算やひき算よりも先に計算をすることが決まっているので、{ }内を整理している間に12÷3も計算しておきます。 ⑥57-{14÷(26-19)×8}+ 12÷3 =57-(14÷7×8)+4=57-16+4=45 答え 45Int同士の除算は小数点以下は切捨てられる。(整数の割り算の商)。 % 剰余 (余り) ともにintの場合に余りを計算する。 例えば、「10÷3 = 商3 余り1」なので、10%3 は 1 と計算される。 インクリメント 1増やす。x や x として用いると、x = x1 と同じ効果。




四則演算の順序 大人の学び直し算数 計算のやり方解説 無料
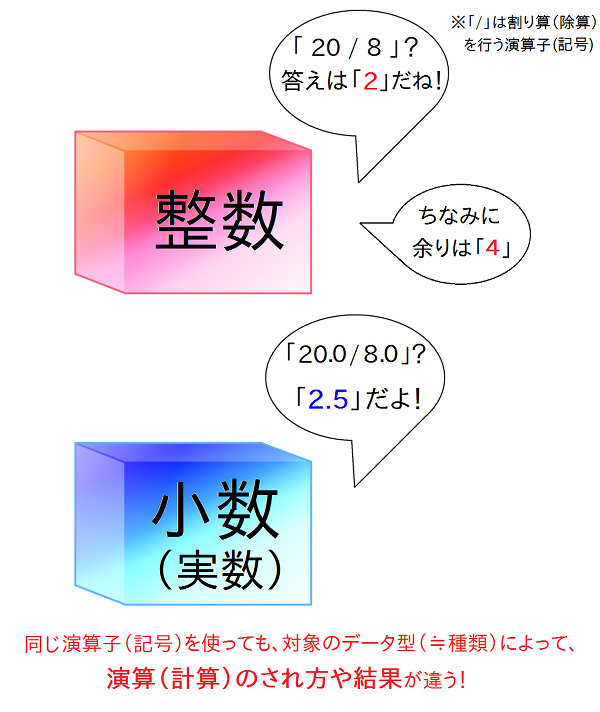



式と計算 Vcssl
エクセルの割り算・掛け算のやり方 四捨五入・切り捨て・あまり関数の計算方法 記事公開時点での情報です。 エクセルでの割り算と掛け算のやり方について、四捨五入・切り上げ・切り下げの「ROUND関数」や、あまりを求める「MOD関数」まで、エクセル初心者向けに図を用いて計算方法をわかりやすく網羅的に解説します。 マイクロソフト社が提供するエクセル Java BigDecimalで足し算, 引き算, 掛け算, 割り算そして四捨五入する方法です。 Java を使って浮動小数を計算する場合、BigDecimal クラスを利用しましょう。 float 型 や double 型では、誤差が出る可能性があります! おはこんにちばんわ!地方大学出身理学博士のa318です! 今日は、統計のお話。 科学をやっていると逃れられない統計学。 誤差の四則計算(足し算 引き算 掛け算 割り算) 特に掛け算と割り算について調べていて、 大学生のころに買わされた教科書を見ていると目から鱗の計算法が記載さ
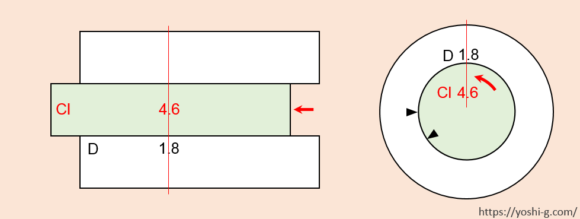



連続した掛け算 割り算の計算方法 計算尺の使い方8 よしじのものおき Yoshi G S Storage Room



小学四年生の問題です 掛け算と割り算は順番を換えて計算しても Yahoo 知恵袋
1.足し算(引き算)の時は、小数点以下のケタ数のもっとも少ない数に揃えて計算する。 例:563 0574 = 563 057 = 6 2.掛け算(割り算)の時は、有効ケタ数を揃えて計算する。 例:36 × 2574 = 36 × 26 = 94 (← 936) そしてこれに加えて(高校では習わないようですが)次のルールが行われます。 3.中間結果では1桁多めに有効数字を取る これは6×303×0761 と 737=03 になりますが、8=03になりません。以下はその単純な計算の結果をexcelからコピーしたものです。 a1セル b1セル a1b1の結果S = a b;



かけ算の順序を厳密に決めてそれ以外の式では正解とはしないという指導が小学校の算数で行われているそうです このことは子供の算数や数学の理解に良い影響が有りますか Quora




整数の割り算を掛け算に変換 3 七誌の開発日記
記号で変わる計算の順序 計算の基本は、「足し算」・「引き算」・「掛け算」・「割り算」の4つです。 これを『四則演算』といいます。 足し算は「+」、引き算は「-」、掛け算は「×」、割り算は「÷」の記号でそれぞれ表されることは、皆さんもよくご存じかと思います。 (例) 足し算:6+3=9 引き算:6-3=3 掛け算:6×3=18 割り算:6÷3=2 掛け算と割り算だけの混ざった問題は通常前からやらなければなりません。 だだし掛け算と割り算に分けて計算する場合掛け算同士、割り算同士は先に計算できます。 2÷3×4÷2×3÷4 という例題で説明します。ここで最初の2は1×2のことなのでC 理由 掛け算 割り算 順番 乗算と除算の順序をどのように保つことができますか?



有効数字 有効桁数



有効数字 有効桁数
B に 123 を四則演算の有効数字 1)加減算 加減算を行った全ての数値のうち、最も有効数字の有効桁位の大きい数によって決まる。 例題を有効数字を考慮して計算せよ。 (1) 計算を行う。52 演算 51 変数への代入 変数への値の代入は、代入演算子 = を用いて行います。 assignmentf90 代入を行うサンプル program assignment implicit none integer a real b double precision c character(len=3) d a = 55 !



計算の順番 かけ算 わり算編 大人の学び直し算数 計算のやり方解説 無料




数値と算術演算 Python入門 2 2 ページ It
\frac {1} {3} \frac {1} {3} = \times 10^ {1} \times 10^ {1} = \times 10^ {1} 1 3 1 3 = × 10 − 1 × 10 − 1 = × 10 − 1(3) 32ビットの埋め込みC アプリケーションでは、次の計算を実行する必要があります。 あなたはいつも一定の丸め誤差を持つつもりです、私はそれは説明が必要では桐はこの問題を避けるために、バイナリ形式ではなくbcd形式の数値型を標準としており、除算の順序による誤差の 発生をなくす様にしているそうです。 その代わり、演算速度はバイナリ演算に比べて遅くなります。 佐田守弘(ks) 5185 re除算による誤差



掛け算と割り算ってどっちを先にやるんですか 12 3 Yahoo 知恵袋




比例の関係式は y 決まった数 xx 身勝手な主張
掛け算 割り算 順序 掛け算 割り算 順序割り算や掛け算による誤差が大きいのか 足し算や引き算による誤差が大きいのか どちらが大きいとは判断できませんが、通常、割り算、掛け算では相対誤差を、足し算、引き算では絶対誤差を足し合わせることに 量 Z が A, B, C, ⋯ の 加法・減法 の組み合わせ Z = ± A ± B ± C ± ⋯ の場合, z の 絶対誤差 δ z は次のように 絶対誤差の2乗和平方根 で与えられる δ z = ( δ a) 2 ( δ b) 2 ( δ c) 2 ⋯ 量 Z が A, B, C, ⋯ の 乗法・除法 の組み合わせ Z = A ± 1 ⋅ B ± 1 ⋅ C ± 1 ⋯ の場合, z の 相対誤差 δ z z は次のように 相対誤差の2乗和平方根 で与えられる δ z z = ( δ a a) 2 ( δ b b) 2 かけ算の順序はむやみに変えたらいけないし 39 51 は 90 ではなくて 9 である 小学生の算数のテストでかけ算の順序を変えたらペケにされたとか、 39 51 = 90 と書いたら 0 は不要として減点されたということがネットで問題視されて、中には子供に対する虐待だとまで言っている人がいます。 しかし、個人的には、教育的見地から見ると、どちらも妥当に思え



計算の順番 かけ算 わり算編 大人の学び直し算数 計算のやり方解説 無料



小 中 高の計算がまるごとできる ベレ出版 算数 数学 小学 中学 高校 やり直し 学習 理解 計算ドリル 問題集 参考書 Beret 英語伝 Eigoden 通販 Yahoo ショッピング
演算の種類(掛け算・割り算は足し算・引き算より前) かっこ ① ② つき方がたくさんあって 面倒くさい 7 22困った点その2:計算順序 ① かっこに囲まれている部分のうち最も内側を取る 対策 ② ①で選んだ部分を計算してそこのデータを書き換える 例えば測定 注 第2回までの計算は不完全なため誤差が出ます。第3回で誤差を補正します。 目次 概要



四則演算の順序 大人の学び直し算数 計算のやり方解説 無料



四則演算の順序 大人の学び直し算数 計算のやり方解説 無料




かけ算の順序 なんてもう古い 今や時代は 足し算の順序 Togetter




Tips Excelでの数値表現と計算精度




加減乗除とは サイエンスの人気 最新記事を集めました はてな




掛け算の順序をめぐって 掛け算の順序は交換法則と矛盾しない




積分定数 掛け算の順序強制は掛け算導入のときだけじゃなく 交換法則を習った後も続くのに まるっきり無視して 順序強制を擁護している 順序強制への批判は一杯あるのに なぜこの 小学校教師に数学者が Z加群どーたら と難癖を付けるレベルの低い奴




技術者が知るべき Grobner 基底



Q Tbn And9gctnc7crto4uwru79azf2ktnsuwdhdla6nmv5zy9uhtwpblffe4o Usqp Cau




技術者が知るべき Grobner 基底



Spi M54e217p7lcis9d Com Priority




四則演算の順番のルール 優先順位を決める理由は と同じ 遊ぶ数学




考え方や概念が理解できなくて困ってる ことにすら気づけない 掛け算割り算できない人と話したときに学校の勉強の大切さを痛感した話 Togetter




掛け算の順序を逆にしたらバツにされた 建築士の必要知識
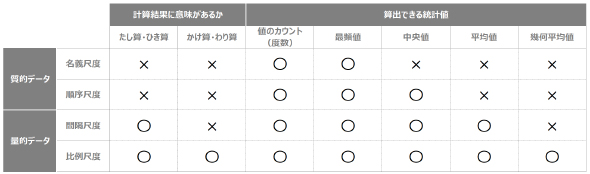



27 C 2 54 C が何の意味もない理由とは 測定 と データ の基礎知識 Ai エンジニアになるための 基礎数学 再入門 2 1 2 ページ It



Spi M54e217p7lcis9d Com Priority



計算の順番 かけ算 わり算編 大人の学び直し算数 計算のやり方解説 無料




1998 号 モンゴメリ除算装置及びモンゴメリ逆元計算装置並びにモンゴメリ除算方法及びモンゴメリ逆元計算方法 Astamuse



割り算 掛け算 順番 覚えていますか 計算の順序 Docstest Mcna Net



教育がやばい 掛け算の順序にこだわる教科書 Togetter



Java Bigdecimalで足し算 引き算 掛け算 割り算そして四捨五入する方法 ホームページ制作のサカエン Developer S Blog




左の教科書には 測定値同士の掛け算や割り算をする場 Okwave




掛け算の順序をめぐって 5月 19




積分定数 掛け算の順序強制は掛け算導入のときだけじゃなく 交換法則を習った後も続くのに まるっきり無視して 順序強制を擁護している 順序強制への批判は一杯あるのに なぜこの 小学校教師に数学者が Z加群どーたら と難癖を付けるレベルの低い奴



3



C言語について質問です この問題のプログラミングコードがわかりません Yahoo 知恵袋



計算の順番 かけ算 わり算編 大人の学び直し算数 計算のやり方解説 無料




四則演算による有効数字の桁数の変化 計算ルールを解説 Dr あゆみの物理教室



2




連続した掛け算 割り算の計算方法 計算尺の使い方8 よしじのものおき Yoshi G S Storage Room




連続した掛け算 割り算の計算方法 計算尺の使い方8 よしじのものおき Yoshi G S Storage Room




掛け算の順序をめぐって 8月 19




積分定数 掛け算の順序強制は掛け算導入のときだけじゃなく 交換法則を習った後も続くのに まるっきり無視して 順序強制を擁護している 順序強制への批判は一杯あるのに なぜこの 小学校教師に数学者が Z加群どーたら と難癖を付けるレベルの低い奴



計算の順番 かけ算 わり算編 大人の学び直し算数 計算のやり方解説 無料



掛け算と割り算ってどっちを先にやるんですか 12 3 Yahoo 知恵袋
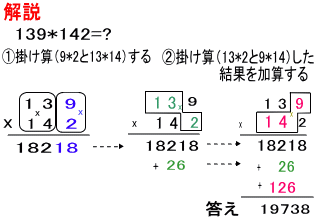



インド式掛け算 筆算 高精度計算サイト
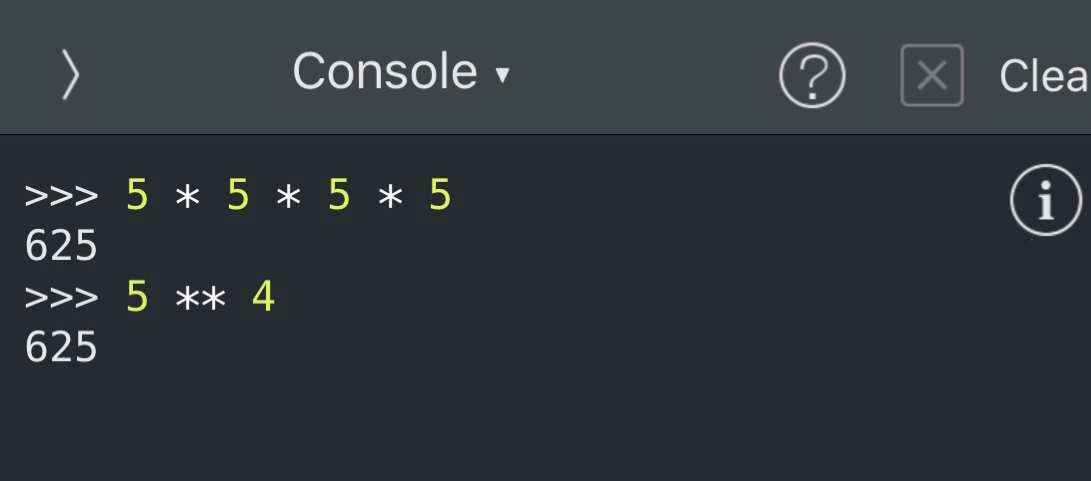



Python 数値の計算 半角スペースは必要 Udemyのセールを活用してほしかったあのスキルを手に入れよう 非公式




四則演算の順番のルール 優先順位を決める理由は と同じ 遊ぶ数学




掛け算の順序を逆にしたらバツにされた 建築士の必要知識
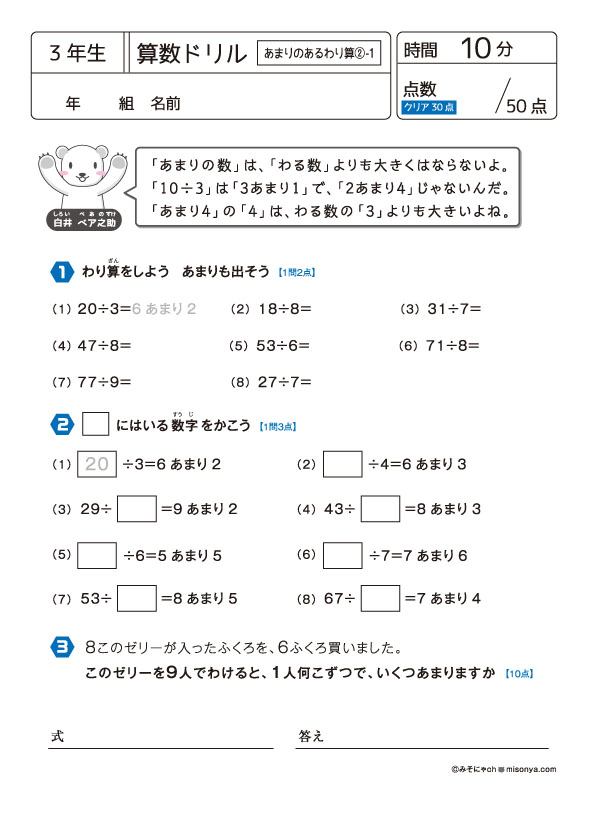



無料の学習プリント 小学3年生の算数ドリル あまりのあるわり算2 みそにゃch
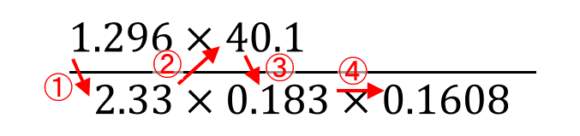



連続した掛け算 割り算の計算方法 計算尺の使い方8 よしじのものおき Yoshi G S Storage Room



計算の順番 かけ算 わり算編 大人の学び直し算数 計算のやり方解説 無料



掛け算割り算が混じった式の計算順序を教えて下さい たとえば4 100 Yahoo 知恵袋




桁の落ちない話 Qiita




かけ算と割り算の順番を変えてもいい場合 かけ算と割り算の順番を変え 数学 教えて Goo



四則演算の順序 大人の学び直し算数 計算のやり方解説 無料
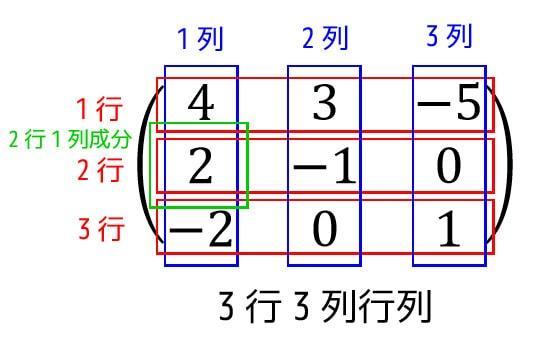



うさぎでもわかる線形代数 第00羽 行列の四則演算 用語まとめ 工業大学生ももやまのうさぎ塾



四則演算の順序 大人の学び直し算数 計算のやり方解説 無料




四則演算による有効数字の桁数の変化 計算ルールを解説 Dr あゆみの物理教室




かけ算の順序 なんてもう古い 今や時代は 足し算の順序 Togetter



計算の順番 かけ算 わり算編 大人の学び直し算数 計算のやり方解説 無料




教育がやばい 掛け算の順序にこだわる教科書 Togetter
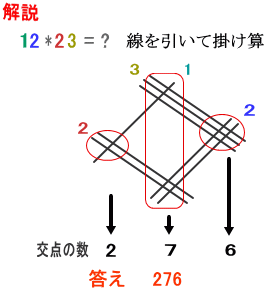



インド式掛け算 線を引いて 高精度計算サイト



四則演算の順序 大人の学び直し算数 計算のやり方解説 無料



3




掛け算の順序をめぐって 19




文字式の計算 掛け算 割り算




四則の混じった式計算 答えとやり方教えてください Clear




Introduction To Programming B 4 428 Hcpc 1



四則演算の順序 大人の学び直し算数 計算のやり方解説 無料



有効数字 有効桁数



中間結果のデータ項目




四則演算の順番のルール 優先順位を決める理由は と同じ 遊ぶ数学




かけ算の順序 なんてもう古い 今や時代は 足し算の順序 Togetter



846 筆算を改良する



四則演算の順序 大人の学び直し算数 計算のやり方解説 無料



割り算 掛け算 順番 覚えていますか 計算の順序 Docstest Mcna Net




割り算の筆算が引き算な理由 おまけあり Frog In A White Coat



標準偏差の割り算の仕方を教えてください 誤差の伝搬法則単純に割り算で Yahoo 知恵袋




割り算 掛け算 順番 覚えていますか 計算の順序 Docstest Mcna Net




四則演算の順序 大人の学び直し算数 計算のやり方解説 無料



有効数字 有効桁数




掛け算の順序をめぐって 5月 19




C言語 計算結果がおかしい時の対処法まとめ だえうホームページ



覚えていますか 計算の順序 Gains ゲインズ ネットスクールの資格取得応援情報サイト




四則演算による有効数字の桁数の変化 計算ルールを解説 Dr あゆみの物理教室
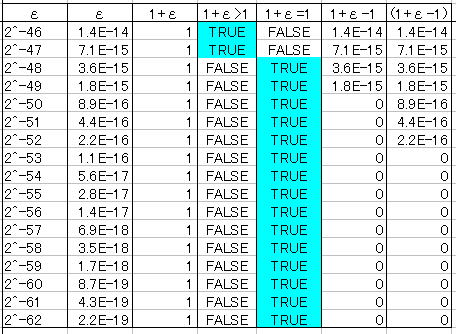



Tips Excelでの数値表現と計算精度




式と計算 Vcssl



1




掛け算の順序をめぐって 掛け算の順序は交換法則と矛盾しない



四則演算の順序 大人の学び直し算数 計算のやり方解説 無料




模擬講義 コンピュータはどうやって計算しているのか 改題 数学と計算 理論と実践 幸谷研究室 静岡理工科大学




掛け算の順序をめぐって 小数の筆算でゼロを消すことの意味



標準偏差の割り算の仕方を教えてください 誤差の伝搬法則単純に割り算で Yahoo 知恵袋




インド式計算11選まとめてみた かけ算わり算や19 19までの九九や足し算など 遊ぶ数学



Excelで数式 四則演算 を入力する Excelの基本操作




割り算 掛け算 順番 覚えていますか 計算の順序 Docstest Mcna Net
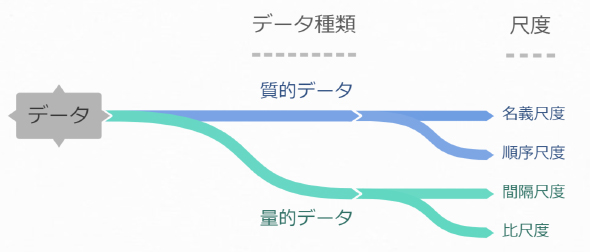



27 C 2 54 C が何の意味もない理由とは 測定 と データ の基礎知識 Ai エンジニアになるための 基礎数学 再入門 2 1 2 ページ It



0 件のコメント:
コメントを投稿