三角錐,四角錐,円錐などの錐体の体積は 1 3 \dfrac{1}{3} 3 1 ×底面積×高さ 底面積が S S S ,高さが h h h である錐体の体積 V V V を求める公式: V = 1 3 S h V=\dfrac{1}{3}Sh V = 3 1 S h の導出を紹介性質 四角錐 長方錐の底面の横の長さを a, 縦の長さを b, 高さを h としたとき、底面積 A は自明なことに A = ab 、 体積 V は錐体の体積の公式から V = Ah / 3 = abh / 3 で与えられる。 直錐の場合、側面積 S は S = a b 2 4 h 2 b a 2 4 h 2 2 {\displaystyle S= {\frac {a {\sqrt {b^ {2}4h^ {2}}}b {\sqrt {a^ {2}4h^ {2}}}} {2}}} となる。 任意の正四角錐は、適当な 直交変換 により、以下の 方程式正四角錐 (點選檢視旋轉模型) 類別 詹森多面體 J 92 – J 1 – J 2 面 5 邊 8 頂點 5 歐拉特徵數 F=5, E=8, V=5 (χ=2) 面的種類 正三角形×4 正方形×1 頂點布局 ( 英語 : Vertex_configuration ) 4(3 24) (3 4) 對稱群 C 4v, 4, (*44) 對偶 正四角錐 (本身)

なぜ 錐体 は3で割る 簡単な説明を 正多面体 から伝授します 横山 明日希 ブルーバックス 講談社 3 4
四角錐の公式
四角錐の公式-三角すいや四角すいのように, 「すい」がつく立体の体積 は, (底面積)× (高さ)× 1 3 \frac {1} {3} 31 の公式で求めることができます。 ココが大事! 「 すい」の体積を求める公式 ようするに, 底面積 と 高さ さえわかれば,三角すいでも四角すいでも簡単なかけ算で体積が求められるのですね。 「柱」がつく立体の体積は単純に (底面積)× (高さ)ですが,「すい ④ 四角錐の体積は? ここで、立方体の体積を思い出しましょう。 一辺がaなので、体積はa 3 でした。 さて、全く同じ形の四角錐6つが立方体に綺麗に収まっていますね。 したがって四角錐1つの体積は、 a 3 ×1/6 となります。 ⑤ 公式を作ろう。
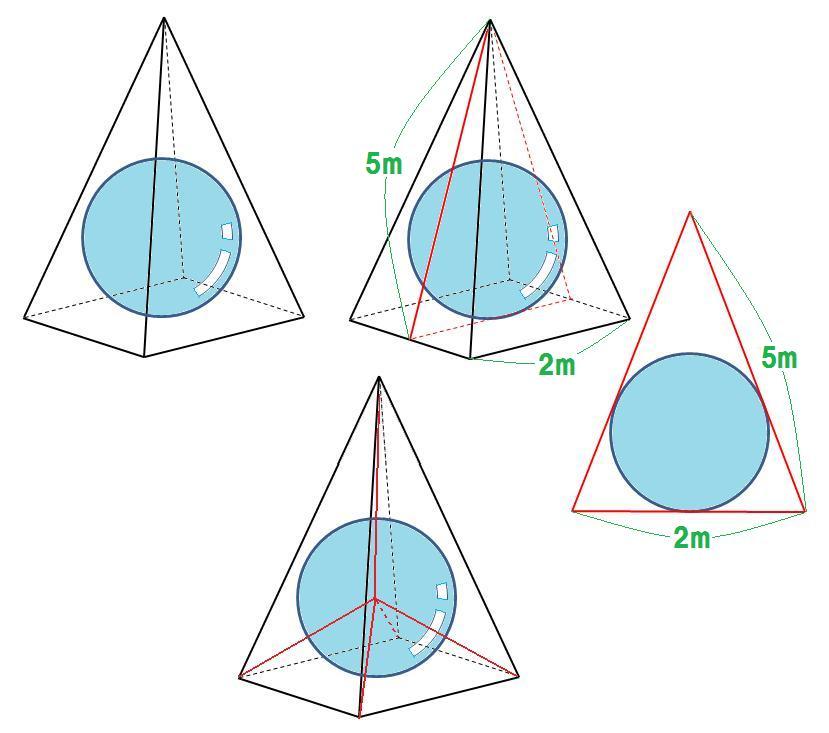



答 正四角錐の内接球の半径 解答集
角錐 P12 角錐台 P12 楔形 P12 直円柱 P12 斜円柱 P12 直円錐 P12 平均自乗誤差 P13 円板の最大応力(σmax)と最大たわみ(ωmax) P96 長柱の座屈 P97 各種断面形の軸のねじり P97 梁の公式 P98 キーの強さ P102 ばねの図表 P111四角錐数 四角錐数 (しかくすいすう、square pyramidal number)は球を右図のように1段目に1個、2段目に4個、3段目に9個、というように 正四角錐 の形に積んだとき、そこに含まれる球の総数にあたる 自然数 である。 つまり 1 から順に 平方数 をいくつか加え四角錐の体積=底面積 高さ 四角錐の体積を求めるときに気をつけたいのは、 必ず を掛ける ことです。
特性 凸 閱 論 編 在 幾何學 中, 四角柱 又稱 四稜柱 是指底面為 四邊形 的柱體,當底面為正方形時會成為 立方體 。 所有四角柱都有6個面8個頂點和12個邊。 對偶多面體是 雙四角錐 。 只要底面是四邊形なので、 まずは正四角錐の高さを求めることから始めましょう。 最初に注目するのは底面の正方形です。 このように底面の対角線を引いて、その長さを求めます。 すると45°、45°、90°の直角三角形ができるので の比になりますね。 そこから、対角線の長さは さらに、その半分の長さ まで求めておきましょう。 次に、正四角錐の高さを含む こちらの直角三角 でした.これは三角錐でも四角錐でも,円錐でも使える公式です. この式に登場する \(\frac{1}{3}\)って何なの?という話をします. 三角形の面積と一緒?? 上に書いた錐の体積の公式とよく似た形の公式があることに気がつくでしょうか?
正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から) 正四角錐台の体積 四角錐台の体積 くさび形の体積 角錐台の体積 角錐の体積 直円柱の体積 一部が欠けた直円柱の体積 中空円柱の体積 斜切円柱の体積 楕円柱の体積 直円錐の体積 斜切円錐の体積 四 角錐 台 体積 四角錐台体積 公式 2月 15, 21 四角すい 四角錐 体積計算 公式 求め方 高さ 底面積 自動 長方錐 方錐 volume四角錐台の体積の求め方 中学一年の者です。 四角錐台の体積を計算する必要がありました。 上記公式に数字を当てはめるとA=43 B=36 a=29 b=19 h=18 単位cmです。 公式に当てはめて計算してみると大方18リットル=10升=?斗であることがわかりました。



四角錐 Wikipedia




中1数学 三角すい 四角すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット
これが四角錐の高さになる。 AMはACの 1 2 なので AM=6 2 ≫ O A C 15cm 15cm M 12 2 cm 6 2 cm OAMで三平方の定理を使うと 15 2 =OM 2 (6 2) 2 OM 2 = OM 2 =153 OM=±3 17 OM>0よりOM=3 17 よって、高さ3 17, 底面積12×12=144 体積 144×3 17 ÷3=144 17 cm 3 ≫類題練習 三角錐の公式が使えるので、 円錐の体積=底面積×高さ/3 になることがわかります。 (別の例) 上図のように、立方体を考えます。 立方体の中心の点を頂点とし、立方体の1つの面を底面とする図形は 高さが立方体の辺の長さの半分の四角錐です。四角錐數 (square pyramidal number)如右圖所示,第一層第二層第三層第四層每層都是 正方形數 合起來是 正四角錐 ,也就是 正方形數 的級數。 例:1, 5(=14), 14(=149), 30(=), 55(=)




計算公式 正四角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
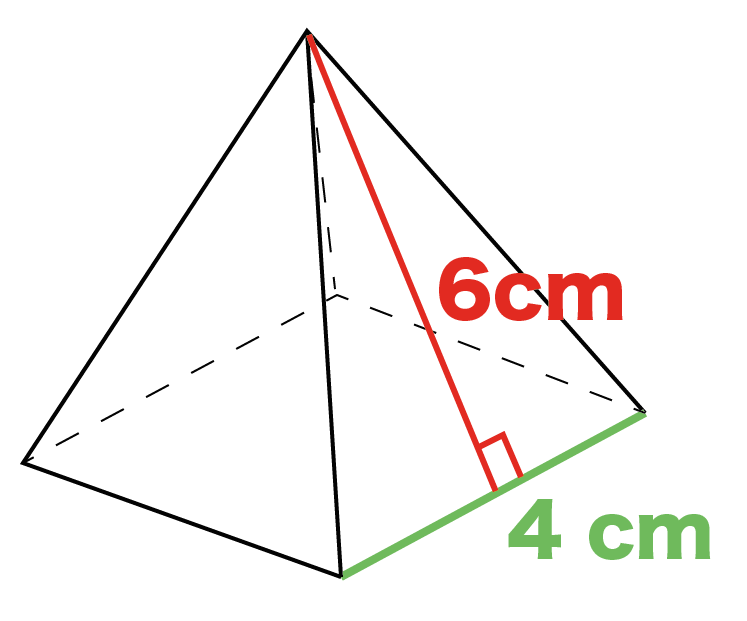



簡単公式 正四角錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
横 b と d )が並行であり, 高さ h の四角錐台 (稜線は 1 点で交わらなくてもよい) (付図 1) の体積: 四 角錐 体積 公式 四 角錐 体積 公式長方錐の底面の横の長さを a, 縦の長さを b, 高さを h としたとき、底面積 A は自明なことに A = ab、体積 V は錐体の体積の公式から V = Ah / 3 = abh / 3 で与えられる。 直錐の場合、側面積 S は = となる。三角錐数でなおかつ四角錐数でもある数は 1 のみである。 三角錐数のうち三角数でもある数は1, 10, 1, 1540, 7140 の5つのみである。(オンライン整数列大辞典の数列 a) 2つの連続する三角錐数の和は四角錐数になる。




四角錐台の体積 高精度計算サイト




3分でなるほど 三角錐の体積 表面積の求め方をマスターしよう 数スタ
四角すい 四角錐 体積計算 公式 求め方 高さ 底面積 自動 長方錐 方錐 volume土塁,土橋,堀などの体積計算に有用であった公式を挙げる.その証明 西村 06 も示す. 公式 1 四角錐台の体積 上下の底面が長方形で,対応する各辺(縦 a と c ;右図は円柱の中が空洞になっているチクワのような形です。 この立体の体積は (cm 3 ) 外側の体積 160π (cm3)から空洞になっている内側の体積 40π (cm3)を引くと V=1π (cm3) 大きな円錐の体積は π×6 2 ×10÷3=1π (cm3) 上端の円錐の底面の半径 ( x とおく)は,比例



四角錐 Wikipedia
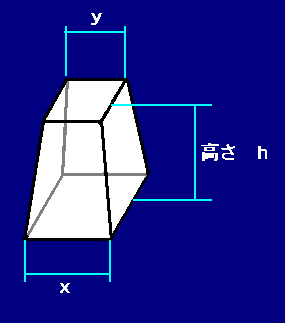



角錐台の体積と平均断面法
④ 四角錐の体積は? ここで、立方体の体積を思い出しましょう。 一辺がaなので、体積はa 3 でした。 さて、全く同じ形の四角錐6つが立方体に綺麗に収まっていますね。 したがって四角錐1つの体積は、 a 3 ×1/6 となります。 ⑤ 公式を作ろう。四角錐台の体積の公式について。四角錐 長方錐の底面の横の長さを a, 縦の長さを b, 高さを h としたとき、底面積 A は自明なことに A = ab 、 体積 V は錐体の体積の公式から V = Ah / 3 = abh / 3 で与えられる。 直錐の場合、側面積 S は S = a b 2 4 h 2 b a 2 4 h 2 2 {\displaystyle S= {\frac {a {\sqrt {b^ {2 正四角錐台の体積の求め方の公式 を紹介するよ。 よかったら参考にしてみて。 台形の体積(正四角錐台)の求め方の公式!? 正四角錐台の下の1辺がa、上の辺がb、高さをhとしよう。 体積は、 1/3 h ( a^2 ab b^2) で計算できちゃうんだ。 つまり、




四角錐の体積の求め方 公式 小学生 中学生の勉強




答 正四角錐の内接球の半径 解答集
角錐や円錐の体積の公式はこれと似ています。同じように、底面積と高さを掛けます。その後、 3分の1にすることで体積が出ます。 つまり、角錐と円錐の体積を出す公式は以下のようになります。 角錐・円錐の体積 = 底面積 × 高さ × $\displaystyle\frac{1}{3}$角柱(円柱を含む)や角錐(円錐を含む)の体積の公式は、皆さんにとって周知のものだろう。 当HPでも 四面体の求積 三角錐の体積 円柱の体積 直交する円柱 角錐の体積 ある図形の体積 切断面の高 シンプソンの公式は単純な積分のみならず、考え方次第では体積を求めるのにも使えます。 今回はその例をいくつか紹介します。 Ⅰ 体積への拡張 Ⅱ 三角柱の体積 Ⅲ 円錐の体積 Ⅳ 四角錐台の
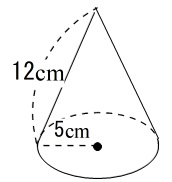



円錐 すい の表面積や四角錐 五角錐の体積の求め方




台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ




公式の証明 体積測定によって検証する土塁の取崩しと土橋の造成
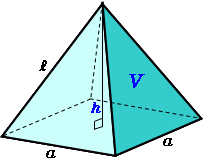



正四角錐の体積 底辺と側辺から 高精度計算サイト




高二空間問題四角錐求高四腳錐求體積金字塔求體積求側面與底面的兩面角餘弦空間問題高二下第一章106龍騰課後卷計算題
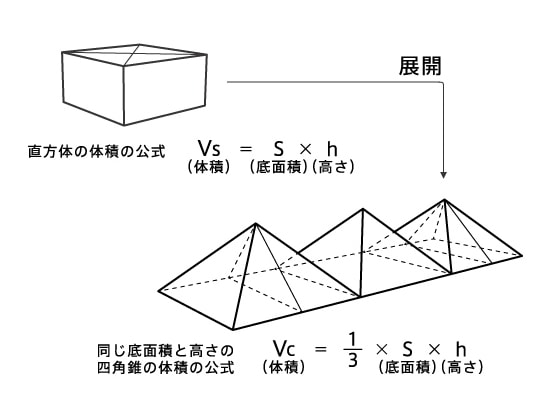



Volume Of A Pyramid 四角錐の体積説明器 Summer すべての商品 ますのび




なぜ 錐体 は3で割る 簡単な説明を 正多面体 から伝授します 横山 明日希 ブルーバックス 講談社 3 4




四角錐の表面積の求め方 公式 小学生 中学生の勉強



四角錐台の体積の公式について この画像のように上下面が共に長方形 Yahoo 知恵袋
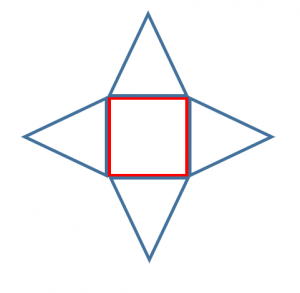



正四角錐の定義 展開図 表面積 体積 具体例で学ぶ数学
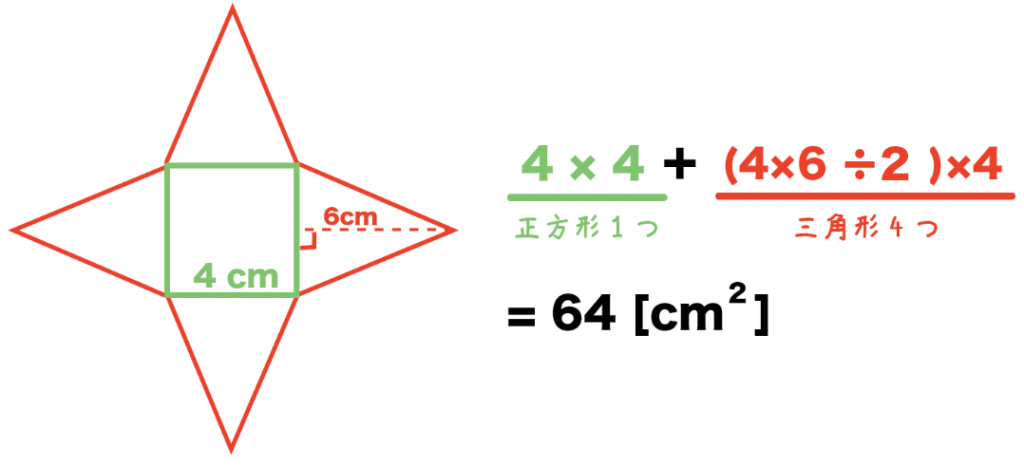



簡単公式 正四角錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




計算公式 正四角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
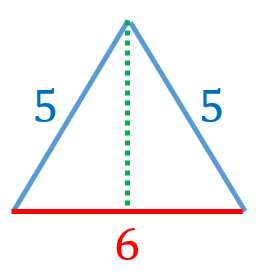



正四角錐の定義 展開図 表面積 体積 具体例で学ぶ数学




56 四角錐の切断と体積 Youtube
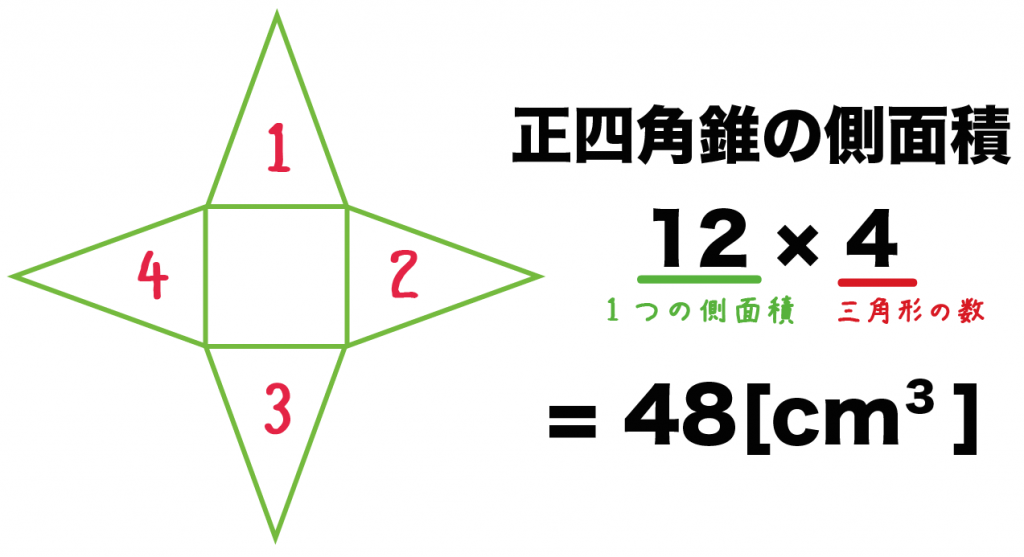



計算公式 正四角錐の側面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




四角錐の表面積 正四角錐の表面積 底面積と側面積を足したら出るよ 中1向けの動画です Studychannel スタディチャンネル 勉強が楽しくなる 学び 動画サービス
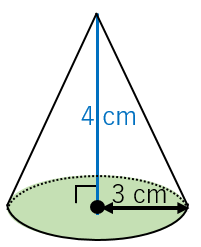



三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学
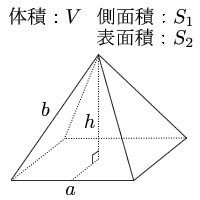



正四角錐 底辺と高さ 体積 表面積の計算 計算サイト



3
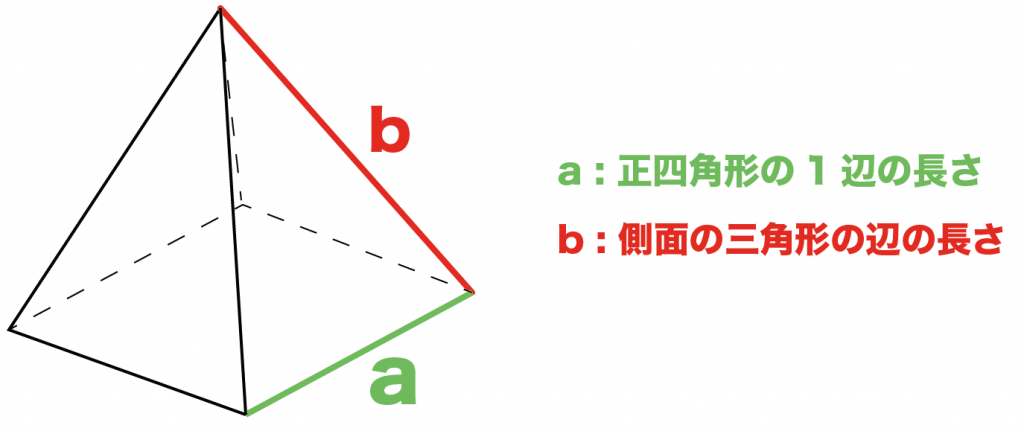



簡単公式 正四角錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




四角錐の表面積の求め方 公式 小学生 中学生の勉強




四角錐の体積の求め方 公式 小学生 中学生の勉強
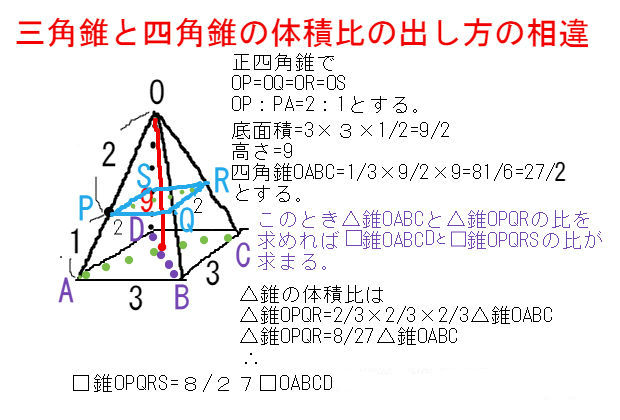



三角錐と四角錐の体積比計算方法の違い 中学数学 理科 寺子屋塾の復習サイト




計算公式 正四角錐の側面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




体積の求め方 計算公式一覧




四角錐の表面積 正四角錐の表面積 底面積と側面積を足したら出るよ 中1向けの動画です Studychannel スタディチャンネル 勉強が楽しくなる 学び 動画サービス




この答えを見て いまいち意味がわかりません どうにか Clear




台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ




四角錐の表面積 正四角錐の表面積 底面積と側面積を足したら出るよ 中1向けの動画です Studychannel スタディチャンネル 勉強が楽しくなる 学び 動画サービス
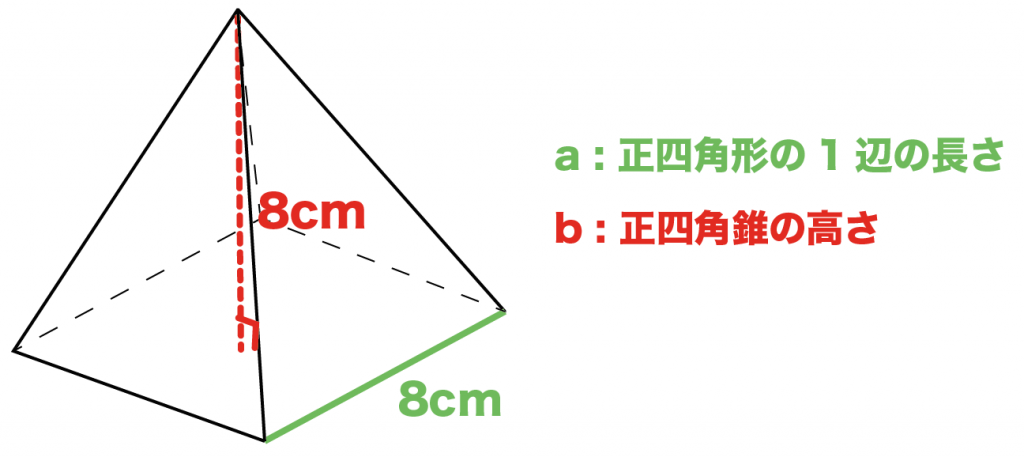



簡単公式 正四角錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




中1数学 三角すい 四角すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




四角錐の体積の求め方 公式 小学生 中学生の勉強
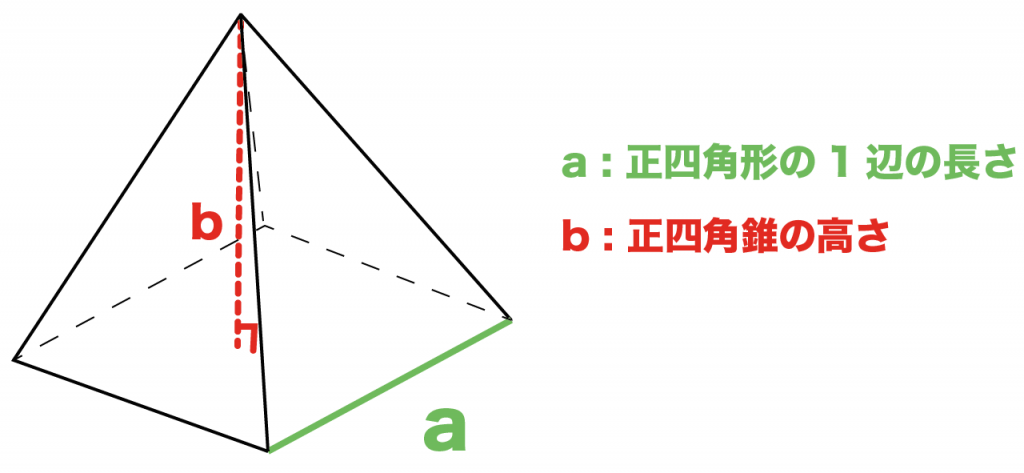



簡単公式 正四角錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
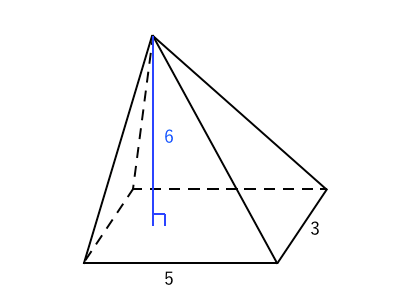



超簡単 体積の求め方 苦手な数学を簡単に
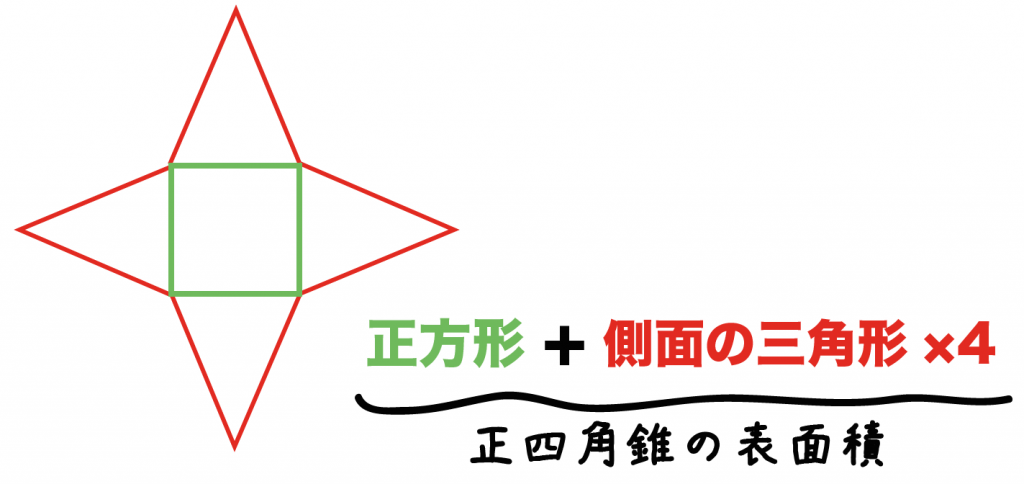



簡単公式 正四角錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




簡単 三角錐の体積 表面積の求め方と展開図が誰でもすぐわかる記事 高校生向け受験応援メディア 受験のミカタ
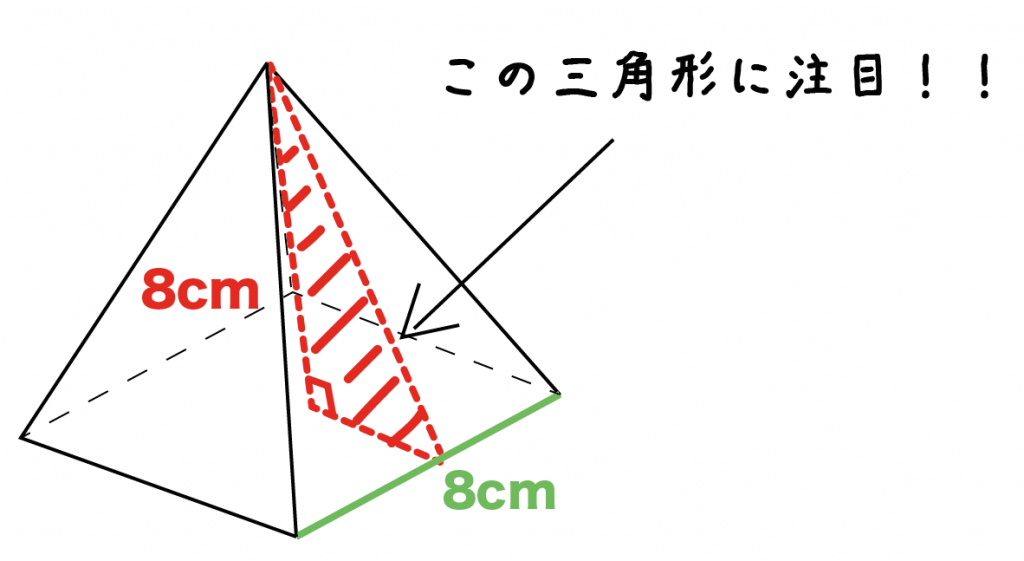



簡単公式 正四角錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



四角錐台 台形の立体ver の体積の求め方なんですが 下面積 上面積 Yahoo 知恵袋
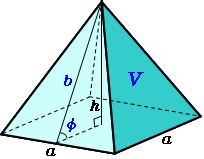



正四角錐の体積 底辺と高さから 高精度計算サイト




計算公式 正四角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
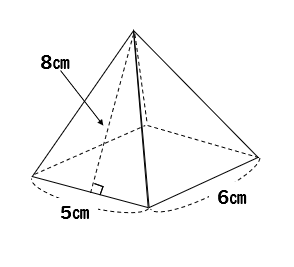



3分でなるほど 四角錐の体積 表面積の求め方をマスターしよう 数スタ




三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学



角錐表面積的計算實例 Live 多媒體數學觀念典online
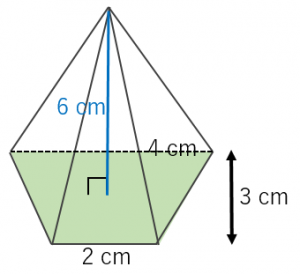



三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学




台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ




実用数学技能検定 数検 على تويتر おはようございmath 本日7月23日は19年4日め 4 は四角錐数です 四角錐 数とは 球を1段めに1個 2段めに4個 3段めに9個 というように正四角錐の形に積んだとき そこに含まれる球の総数にあたる自然数のことです




計算公式 正四角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
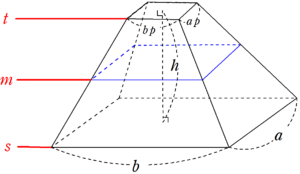



シンプソンの公式 応用編 Fukusukeの数学めも




正四角錐の定義 展開図 表面積 体積 具体例で学ぶ数学




四角錐の体積の求め方 公式 小学生 中学生の勉強



計算公式 正四角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
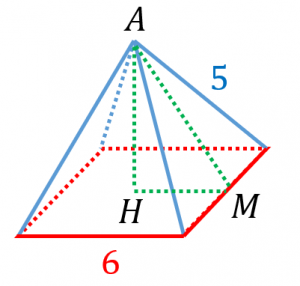



正四角錐の定義 展開図 表面積 体積 具体例で学ぶ数学




四角錐o Pqrsの体積を求める問題です 青く囲った部分の式は公式ですか Clear
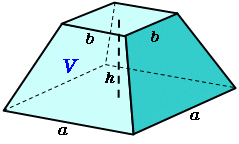



正四角錐台の体積 高精度計算サイト



Math 角錐の体積が角柱の3分の1になる証明 働きアリ The 2nd




つぎの正四角錐の側面積 高さ 体積を求めてください 三平方の定理です Clear



簡単公式 正四角錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




四角錐の表面積の求め方 公式 小学生 中学生の勉強



1




四角錐の表面積の求め方 公式 小学生 中学生の勉強
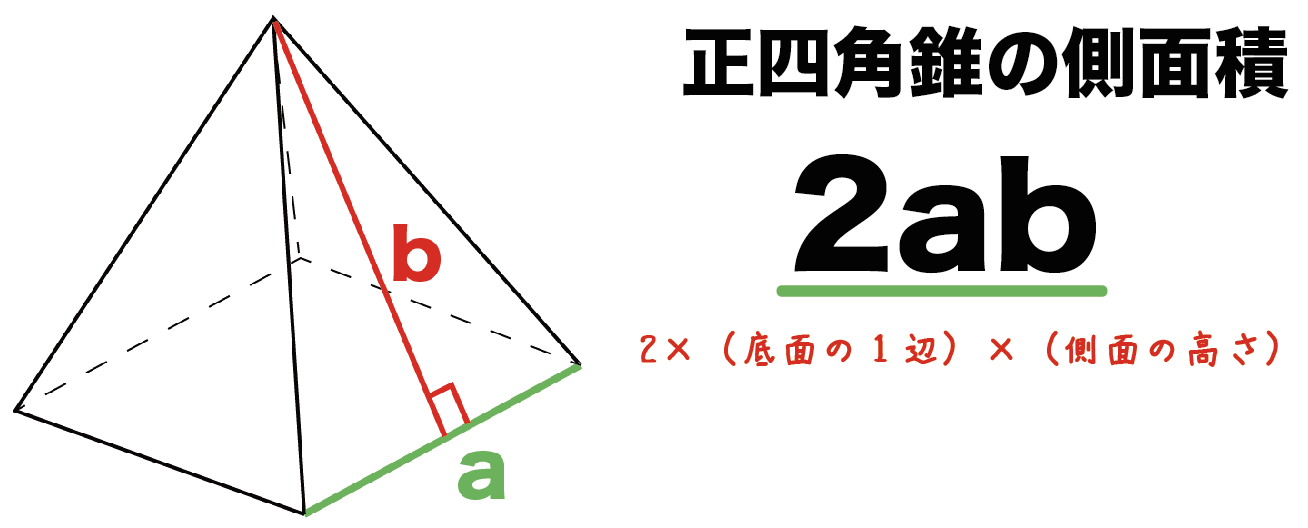



計算公式 正四角錐の側面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




高さの分からない正四角錐の体積を求める方法をイチから解説 数スタ




計算公式 正四角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



1




公式の証明 体積測定によって検証する土塁の取崩しと土橋の造成



中1 空間図形 4 立体の表面積 2 学習支援 まなびの函




角錐 円錐の体積と表面積の公式 数学fun




どうして1 3なの 錐の体積の公式の求め方 まなべーと




台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ




体積の求め方 計算公式一覧




三角錐 四面体 の体積の公式 Schoolmath S Diary




四角錐の体積の求め方 公式 小学生 中学生の勉強




角錐 円錐の体積と表面積 計算ドリル 問題集 数学fun




四角錐 Wikipedia




四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後




高校入試 三角錐と四角錐の切断 Youtube



1




三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学




角柱 円柱の表面積と体積の公式 数学fun



四 角錐 台 展開 図




表面積の求め方 計算公式一覧
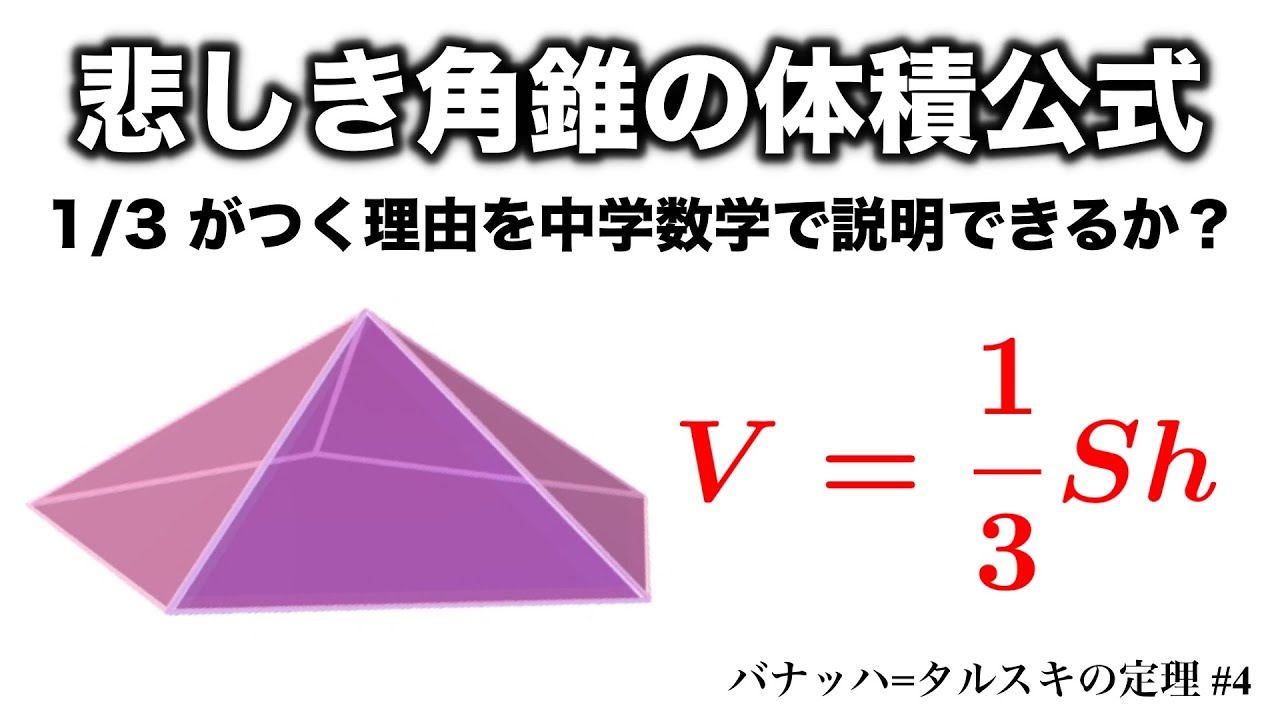



悲しき角錐の体積公式 1 3 がつく理由を中学数学で説明できる バナッハ タルスキーの定理 4 Youtube



この写真の正四角錐の高さの求め方教えてください 四角錐の体積の公式 Yahoo 知恵袋




公式の証明 体積測定によって検証する土塁の取崩しと土橋の造成




錐体の表面積1 例1正四角錐の表面積の求め方 Youtube




3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ



四角錐台の公式 体積 側面積 表面積 数学 エクセルマニア




どうして1 3なの 錐の体積の公式の求め方 まなべーと




四角錐の表面積の求め方 公式 小学生 中学生の勉強




公式の証明 体積測定によって検証する土塁の取崩しと土橋の造成
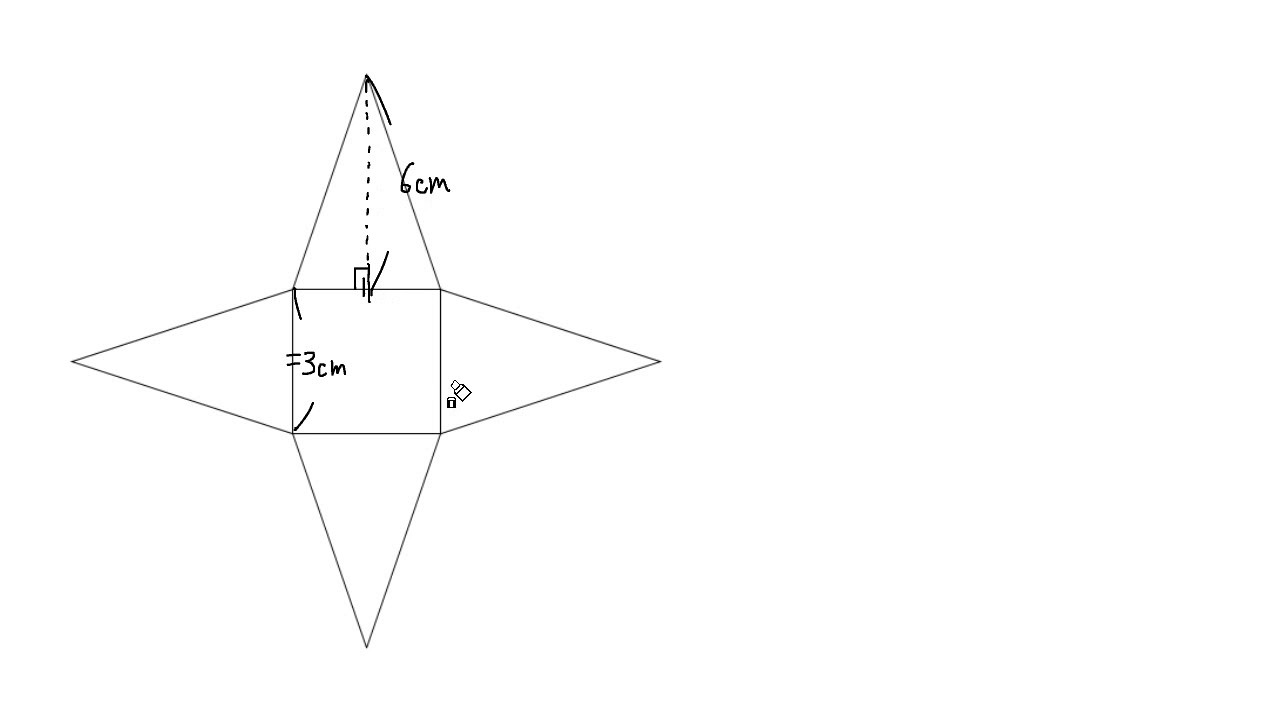



正四角錐の表面積 Youtube
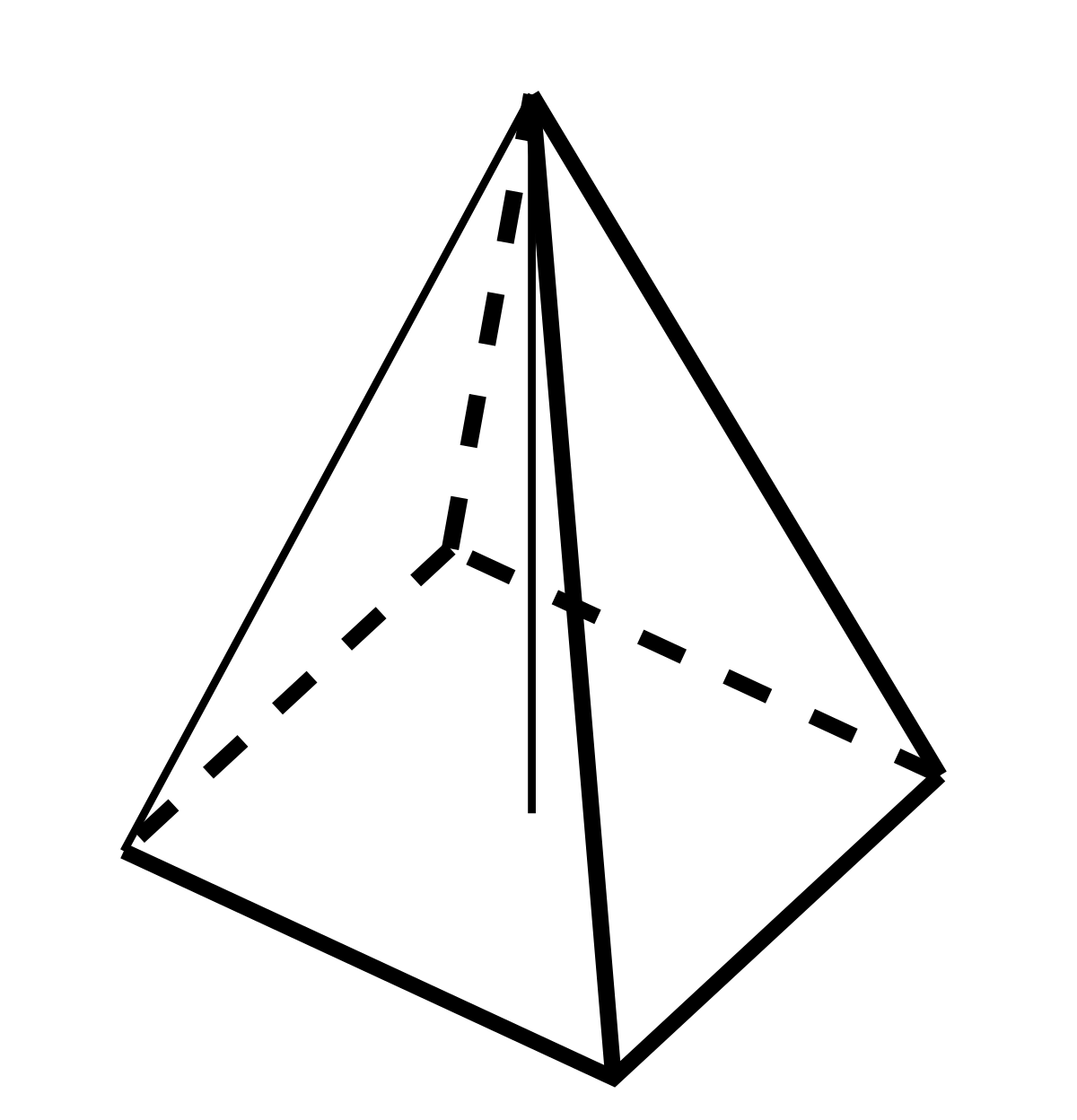



四角錐 Wikipedia




角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学




中1 中1 数学 円錐 四角錐 正四角錐の公式 中学生 数学のノート Clear



0 件のコメント:
コメントを投稿